
最近出走予定
(済)…支払い済み
(未)…支払い未だ
消防設備士甲種1類 2026年2月8日(日) 札幌 会場試験 (済)
↑甲5受けようかな、と思ったけどやめた。
日本漢字能力検定 準1級 2026年2月15日(日) 札幌 会場試験 (済)
令和7年度第三種電気主任技術者下期試験 2026年3月22日(日) 札幌 会場試験 (済)
↑理論が消えない内にいきたい。「電力」と「法規」を落とします。
以上 2025.12.10 更新
2026.1.22 更新
とりあえず、佛教大学の教職課程やろうかな。どうするかな…2年で50万くらいかかるんだよな。まあ、イギリスのより全然いい(安い)けど、私の歳になると普通のケースでも教育実習先がね。それより、相補完理論だけども「私に教えないんだったら数学の間違い探しでもやっててくれ」と言ってたけど、もうそろそろ見つけたかね?、私も言った手前、物理と被ってるけど、無限小の微積分辺りを語ってるけども、要するに高校でやる「複素数平面」というのは、微積分であり相対論(の修正)であり、全てだったんだね。あれは複素数平面上で回転するわけだから、あれが回転宇宙論という事だったんだよね。数学の座標上の回転はあくまで抽象的な回転であって、物理で整合性を取ると、無境界領域での回転、そこでは方位も一つしかないところを無時間で超えているので、全方位同時回転からの物質化、つまり、正負の運動量(回転)で二種飛び出す(物質、反物質)という理屈だったよね。それで、1とか0とか虚数の定義の話だったわけだ。2乗してマイナスになる数の発明というのは、重要なのは実数数直線上に乗らない数という事だ。
つまり、ユークリッド空間というのは、複素数(平面)を加えてやって、完成をみるということ。底面があっても、高さが(高さの次元が無いので)伸びていかないんだよね。我々の存在空間を三次元空間と認識してそれを前提としてユークリッド原論の定義を語っているけど、それだと不完全だ。故に、ユークリッド空間だ非ユークリッド空間(← 数学)だ、という議論の前に、ユークリッド空間をもっと吟味し完成させるのが先だった、ということだ。
直線と直線の挟む角が直角になって、それで構成されるのが面、そこから直角で立体…という定義は、そういう風に次元の定義を決めたのではなく、次元の定義とは虚数が実数軸と直交しているところからその定義を求めるべきなのです。ゆえに、物理の次元論として、曲がっているとは、その直交している所から見て曲がっている、という風に厳密に定義出来る。
↑全方位回転も分かるよね。入ってくる時はどこかしらかから入ってくるけど(素粒子衝突)、回転エネルギーの慣性が出てくる時に無境界に入るがそこは無時空間(虚時空間)なわけだから、逆回転をも含む全方位に回転するわけだよ。無境界は虚数時空間だったね。回転力が帰ってくるけど、どこかしらに向かって回転するから回転エネルギーであって(ここではポジションと未分化)、それはここでは全方位以外取りようが無い。全方位というのは、数学の抽象的な複素数平面で言えば、iを4つかけて回すという意味。それが同時に起きるので物質化が起こるという理屈。
*故に、物質と反物質は、正負の運動量は必ず相殺され、ポジションも相殺されます。物質と時空間は切り離せない、つまり前次元が抽象的という意味ですよね。
↑もう、これで、『スタディジョッキー』は私の監修でいい。現地の受験問題に対する対応とかは、他のスタッフがやればいいだろ?私はそれは知らんよ。私はあとは、全体的な設計とかさ。以前も言ったが歴史上の天才達はちょっと、ゲームにするのも各国民衆心理的に「(営利に利用して)どうかな?」という意見が多かろうから、彼らを使わなくたって面白いゲームだと再三言ってるじゃない?私も歳なので、語っていたことを何も実現せずに死んでしまいかねないので、ちょっと頼むよ。私が監修だったら嫌だ、とかじゃないよね?↑基本的に現地国の受験に対応するかも怪しいよ。
中堅高校で「春巻高校」という話だったけど、こういう設定を他の研究者とか大学の先生に出来るとは思えんね。
佛教大学で↑『スタディジョッキー』の研究を深めようかなと(佛教大学は一応、数学教職目指したり教育論とか読んだ方がいいかな?とね。でも金がね)
私は内心インドの政治家には「日本の問題だししょうがない」と言いつつも失望している。まあ、またインドのレストランを訪れに旅行する時もあるかもしれませんね。
インドの時の『Isystem』もそうだけど、私の人権も重要だからさ。イベントでファンを集めて、もう日本の某組織みたいな、まあ実のところ某組織だけなのか、下劣な下い話は一切止めましょうよ。一切ね。
2026.1.5 更新
だから、↓大丈夫だって。私も被害に遭って辛いとか、忙しかったりであれだけど、(札幌なので)北大の数学科の院生が大学院の合格問題集を解けるくらいやれば出来るって。北大の数学科の先生達とは言わんよ?
『スタディジョッキー』の話だよ。大学1年くらい(微積分、線形代数)のやつまでをゲームにするだけじゃないの?、勉強嫌いの(私は好きでも嫌いでもないかな?)子供、未成年達に届けるのが使命なんだよ。どこかで開発に着手してもらえないかな。日本でやるのは難しいことは再三述べているが、日本の数学検定の例で言うとだな、準一級や一級を中学生時に合格するようなのが本ゲームで量産されるのだ。大学受験にも良い効果があるだろうし、ちなみに「大学なんてどうでもいい」と言う意見もありそれは正しいのだが、あくまでも”大人の見地”からだ。大人だったら大学なんてもう終わった話なので、どの大学でも良かろう?(自分の大学でなくて「東京に在る大学の学生生活が良かった」と言ってもどうにもならないのだ)、未成年だったら、学問内容や生活内容、年収も変わってくるし、どうでも良くはないだろう?、あくまでもよく耳にする「大学なんて知ったこっちゃない、どうでもいい」と言うのは大人の見地であることを留意しなければならないよ。サッカー選手になりたいのに「サッカーじゃなくていい」とかおかしな話だし、そんなはずないだろ?それに「レギュラーで」と、コンサドーレとリバプールに誘われているのに、どっちでもどうでもいいと言うのも変だろ?リバプールの方が良さげだろ?まあ、そんなに札幌がいいというのなら話は別だがね。
↑という事だから、「ハルマキ高校(仮名)合格特別」とか、まあ、中堅クラスの高校かな。馬走らせて超楽しいじゃないの?、出走条件を満たすべく問題集を解かないとね。レース場コースから高校が見えますよ。在校生達も応援に駆けつけています。『頑張れ〜』みたいな。「馬の調教が数学の問題集を解くこと」ってウケるよね。私の監修でいいって。あとは、問題作ったり分析するのは他のスタッフでいいだろ?
2026.1.5 更新
くどいけど、無限小というのはシンプルに考えて、C(定数)/ ♾️ とした場合、これに♾️をかけても不定形になるのではないかな?、それに何をかけてもC(定数)/ ♾️ に A(定数)をかけても、結局 C(定数)/ ♾️ ということで、意味が分からない。無限小が数直線上で0から無限小まで一定の幅を有するとすると、その幅を際限なく小さく出来るので、それはその幅が無限小であることに反する。ゆえに、無限小なるは0からの幅を有してはならない。つまり、0ではないが幅を有さぬ値、のような感じで、幅がないところから積み上げて有幅までもっていけるもの、という風に定義してしまっているのだろう。しかし、してしまったと言われてもだな、「C(定数)/ ♾️ に♾️をかけても不定形」を無視しているのではないかな。
ユークリッド原論の冒頭部の点の話は、実は0とか1の話であって、点から点を起点に線を引く、というユークリッドの話は、実は自身が存在している(と認識していたであろう)3次元空間を前提としていて、そもそもの話、数直線上の数というのは、あれが一個二個…と、何かしらが”有る”わけだから、それが実数なんだよ。つまり、ここのユークリッドの冒頭部がニュートンであり相対論でも有る話なのだから、
- 点とは部分をもたないものである。
と言われても、あっさり次に行ってはならない。点から線を引いているけど、点というのは(数学的)三次元空間と、点からシャープペンシルで線を引くという所作(物理的な時間)はどうなのか?とか、ならば、我々がシャープペンシルで白紙に打つ鉛筆跡は点なのか?、これは部分がある(鉛筆線とは部分を繋いでいるにすぎない)。部分がないところからどうやって線に(長さ)なるのかなぁ?と、部分が無いところの連続が線で有るという話なので、部分が無いところに部分が有るものがやってきて線を引くのかな??、部分が有る人が点を打ってもやっぱり部分が有るからさ。みたいな話になって、話が決着しないんですよ。それで、微積分のワイン樽の話が出てきて、まあ、これは例えば、線から面に、面から立体にするやつかな?と、でも、無限小ってなにさ??と、それで虚数概念が出てきて、「それだ」となる。虚数軸が任意で垂直に立ってるよね、と。虚数を実軸化して実任意微小片(例えばdx)を作りしめ、それにより点から長さを生み出す操作が可能となり、それが積分だ、となるのです。
結局のところ、「C(定数)/ ♾️ に♾️をかけても不定形」を無視しているから、数学でもさらには物理でも詰まったと言えないだろうか?↑この議論に、限界時間とか必要ないだろう?
2026.1.5 更新

↑これは私が買った高校の数学の公式集の冒頭部だけれども(『モノグラフ』(矢野健太郎著 科学新興新社))、これだと整数から0が出てくるような印象を受ける。一番左側に「0と虚数」を持って行って、そこから→ 「複素数」(実数、虚数)ではないかな。0は一番左だろ?数の分類で「数が無い」という意味。虚数は「無いけどあるって事で仮定しようかな」→ 複素数(数が有る。実数が出てきた)
数学の慣習的に「0」は整数に含まれるのかもしれないけど、0/3 = 0、とか分数でも0があるじゃない?「ただ、自然数や負数を述べるためにそう書いたんだろ。左側に含まれるよ」と思うだろうが、「有るって事にしちゃおうかな」が、今までの話を鑑みると、数の分類表として好ましい。数として一番左に「実数、0、虚数」(複素数)となってるが、
0 → 虚数 → 実数 … というかさ。話というか主張がよく分からなければ、上の表で、「数(複素数)」と書いてある箇所と「虚数」と書いてある箇所を入れ替えればいいよ。大体、実数のルートの負数の概念から拡張されたのが虚数だろうから、虚数は実数より左側に来るべきではないか?
「小学校から高校〜大学教養課程レベルまでの『スタディジョッキー』って何さ。どうせ、学者が書いた市販の公式集をモロパクりなんでしょ?」と思うだろうけど、↑冒頭からして違いが出ている。点(0)が包含している任意の虚数軸から次元拡張(実数軸、一次元)しようかな、という話と結びついている。確かに、実数は3とかで、虚数が2iであるから、3+2i が複素数なので、複素数が一番左に、としてしまうが、一番左が「虚数」として、その隣が、実数化出来る虚数(つまり実数)と、出来ない虚数(虚数)と実数との混在(複素数)だろう。
細かいけど、そういうことだ。私もこの著者の矢野先生のようにまた、パリ大学に戻ろうかな(←私は以前にちょっと訪問しただけデス)。ちなみに、この公式集の監修者の矢野先生は東大卒でパリ大学卒だけど、若者達も、東大は昔は当然、日本の権威というか頭が良かったんだろうけど、今は腐って泥棒(公金)強姦ないし拷問の役人集団のイメージしかないよ。私の新潟の大学の時の担当教官も学部長もたまたま東大卒だったし、そういう流れで頭がいい大学の例として、私は日本ではよく「京都大学」を例示しているが(←日本では異論ないだろう)、それは東大にウンザリ来ているからだ。言わなくても分かるよね。「いや、京大でも他の難関大学でも役人は多いだろう?」と主張するかもしれんが、役人は東大さんだろ?この大学は日本がとんでもないことになってしまった責任を取るべきだ。
今度は中国かな?みたいに言ってたけど、なんか中国は恨んでいる少数民族が多そうで、私は思想とか太極拳とかのイメージで嫌いじゃないんだけども、あんまり対立軸に乗らない国が好ましいよ。それがハッピーライフでは重要な事。平和で非暴力、そして愛されるという事。これが人間にとって大切だ。
2026.1.4 更新
いや、やっぱ、佛教大学は要らないかな…。これはあくまで教職を取る目的のようだし、実習訓練先が無い可能性が十分あるよね。数学のレベルも放送大学と大差ないかもな。というか、大学の冷酷さというかもう嫌気がさしてるよね。つまり、自分の研究機関としてここは『スタディジョッキー』を開発してもらって、そこの建屋で数物をチンタラ研究するみたいな感じにする他、もうないのかもしれない。
スタディジョッキーは数学の大学の先生に乗ろうと思ってたけど、誰も話しかけてこないし、数学も自分でやるしかないのかな…。私の話を考慮すれば、いかにユークリッドの定義があやふやか分かるだろう?原語で読んでないけど(日本語訳ですが)、「点とは部分を持たないもの」と言ったって、大きさが無いのか(無点)、分け隔てられる部が無いのか(単一)とかさ。やはり、数学的な次元拡張を吟味すると、数直線上には無限の数が存在しているわけであるから、数直線上において「0の隣は無限小」的な曖昧さを排除するならば、物理から導かれたものと同様、虚数の(実数軸に垂直に立っている)の実数化という操作こそが微積分という事になるはずだから、これは物理と同じ。次元が上がる時に実体化する。幅の無い長さを積み上げても、幅が生まれないし面にならない。つまり、限界小と回転宇宙論から虚数の具現化にたどり着いたが、これが次元の上げなんだから、つまり数的な宇宙(1)と(1以下の数)からして、同様に、虚数とは数直線上にない数、つまり、これは微積分学の要請から必然性を持った「数」だったんだね。虚数を実体化させて積分素、例えばdxを作り出すという操作こそ積分だ。
くどいが、幅がないものからどうして幅が生まれるのかという話だ。0から積んでやっても0.000…1になれないんですよ。
↑これはフィールズ賞だね。私もいいこと言えてホッとしている。ノーベル賞でも取ろうと思ったら取れる、とネタで行ったたけど、「それではフィールズ賞も取ろうと思ったら取れるのか?」「そう思えば、必ず取れます」と言ってたけど、内心はヒヤヒヤでしたよ。「ちょっと数学の数式めっちゃムズイよ」みたいに数学の本見て思ってたけど(ドキドキしていた)、何とかあたりをつけれたというか、数学は厳しいよね。
2025.12.31 更新
「まあ、両親介護や金銭的事情等により気軽に海外に来れないのは理解出来るが、日本に居てもしょうがないじゃん?」 という海外で心配なさってくださる声もあるかもしれないですが、とりあえず、先に申したようにイギリスの通信大学は金銭的事情より退学する事にして、代わりに安いやつを、秋田大学通信や佛教大学通信の「教員免許状取得課程」をやって数学教師になろうかな?と思っています。もう歳だし、教育実習先がなかったら無いでしょうがないかな?と、ネタのスタディジョッキー的にいいかなと思って。インドの時に『Isystem』がどうこう言ってたけど、とりあえず数学でもやってます。別に海外に行っても私の主張している人権問題が進展する感じでもなさそうだしね。
もう歳だし被害者だし、日本で学校の数学の先生になろうなんて思ってないよ。そもそも3浪で未成年達に京都大学の合格をレクチャーしたくないよ。↓
私 「いいか。京都大学(広く難関大学の意)に受かるにはだな…」
高校生 「(シラーッ)…」
高校生 「この授業内職します」
私 「ああ、高校生達に見捨てられてしまった…」
…
まあでも、やったらどこかで教育実習だけは用意して欲しいよね。でないとその課程を修了出来ない。
なんかどっかで、日本以外で『スタディジョッキー』やりたいみたいな組織無いの?
2025.11.18 更新
インド渡航を終え再び日本に戻って来たので資格取得も再開します。今、消防設備士から仕事を探しているので残りの「消防設備士」、さらに理論だけ受かった「電験三種」、悲願の「社会保険労務士」などを考えています。
他にも、
基本情報技術者試験、司法書士試験、数学検定準1級及び1級、イギリスOPEN大学物理科(株の大ダメージで金が無いので勧められない。GREのスコアに励むだけでいいかな?と思い始めています)、秋田大学総合環境理工学部材料工学基礎コース通信講座(イギリスの大学の代わりでやろうかな、と。こちらは比較にならぬ程安いです)、edX MicroMasters International Law UCLouvain(オンラインで学習出来る人権学等で構成されるコースです)、TOEIC800点、漢字検定準一級、フォトマスター検定、ERE経済学検定試験…辺りを狙っています。
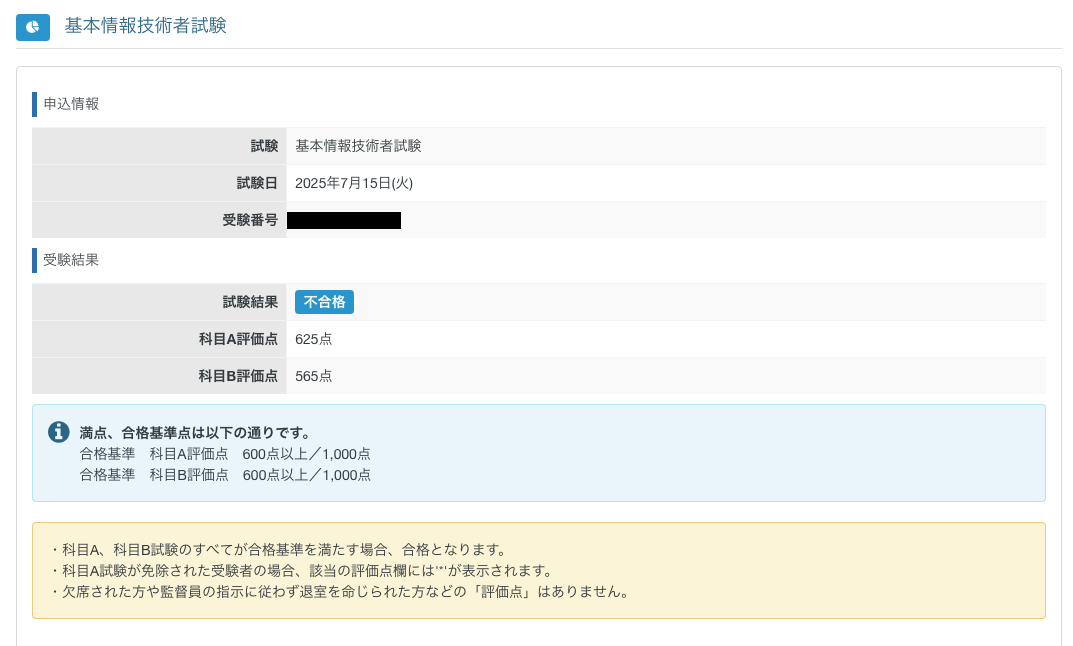
↑基本情報技術者試験の方は次で受かるかな、と思います。
【保有資格】更新 2025.12.4
・大学学士(放送大学教養学部通信課程) (2006/9/30)
・日商簿記2,3級、(1級がないのがショボイ) (2009/11 三級、2010/6 二級)
・IC3 (IT系資格。取れて良かったが、簡単) (2006/9)
・MCAプラットフォーム(取ったのにMCA資格が終了してしまった。これが民間資格のいやらしい所) (2006/10)
・フォークリフト技能講習終了 (ペーパードライバー)
・タイ式マッサージスクール コース終了 (終了しただけ。大してもみたくない)
・剣道三段 (やっと男になれた気がします)
・証券外務員二種 (収入も無いので実際株取引をしたくない。置かれた環境により不確定要素が強すぎて出来ない) (2010/11)
・TOEIC 520点 → 530点 → 545点 (2016.1.15) (伸びが無い...。もっと取れそうな気はしていたが、この点数はあまりにもリアル)
・Oracle Certified Java Programmer, Silver SE 7 (2013/11/23) (オラクル社のJAVAプログラマー認定資格。久しぶりに一回でウカッて良い感じ)
・JAVAプログラミング能力認定試験2級 (2014/1/26) (サーティファイのJAVA資格。結構忘れていたが合格したので簡単。とりあえずでもアピールするならば1級でなければ、と思った)
・漢字検定3級 (2014/2/2) (1級合格はまだまだ先か...)
・ITパスポート試験 (2014/3/9) (小型資格を集めて一体何なの?...とは言わないで。ちなみに、試験場でコラボレーションキャラクターのクリアファイルをゲットした)
・漢字検定準2級 (2014/4/12)
・証券外務員一種 (外務員登録無し) (2014/5/1) (株も買った事ないけど、取り合えず資格だけ)
・数学検定3級 (2014/4/20)
・放射線取扱主任者第二種 (2014/10/20) (試験だけ。二種の講習はいつ受けてもいいそうで、でも高いので...)
・第三種電気主任技術者 科目合格(一科目)(2014/10/22)(2年経ち合格科目が失効した...)(2016/9/20)
・危険物取扱者乙四種 (2015/2/20)
・FP技能士3級 (2015/3/5)
・ボイラー技士2級 (2015/4/27) (試験だけ。講習は5月に受ける予定。*2015年5月に免許取得済み)
・HSK(中国語検定)1級 (2015/5/7)
・数学検定準2級 (2015/5/7)
・危険物取扱者乙三、六種 (2015/6/19)
・第二種電気工事士 (2015/9/4)
・危険物取扱者乙五種 (2015/11/19)
・エックス線作業主任者 (2016/3/17)
・危険物取扱者甲種 (2016/6/15)
・FP技能士2級 (2016/6/29)
・数学検定2級 (2016/8/9)
・漢字検定2級 (2016/9/16)
・札幌シティガイド (2016/10/28)
・茶道文化検定3級 (2017/1/11)
・消防設備士甲種4類 (2018/3/1) (合格が切れて禁断症状が出ていたので、補充出来て嬉しいです)
・特別教育終了証『足場の組立て等の業務に係る特別教育』 (2018/2/27 交付)
・安全衛生教育終了証『丸のこ等取扱作業者安全衛生教育』 (2018/2/27 交付)
・消防設備士乙種6類 (2018/4/18)
・消防設備士乙種7類 (2018/4/18) (これからは「設備士」を名乗ろうと思います)
・統計検定3級 (2018/4/28)
・風水アドバイザー (2018/4/28) (某通信講座の認定証を取得しました。ようやく資格的に(?)風水師になりました)
・メンタルヘルス・マネジメント検定Ⅱ種 (2018/5/1)
・測量士補 (2018/7/10)
・北海道観光マスター検定 (2018/12/12)
・MIDI検定3級 (2018/12/14)
・メンタルヘルス・マネジメント検定Ⅰ種 (2019/1/11)
・林業就業支援講習終了(5日間コース) (2019/2/16)
・普通自動車第二種運転免許 (2019/4/22)
・潜水士 (2019/10/8)
・大学院修士(高野山大学院密教学部通信課程) (2021/3) やらなければと、期中放置のようになったが、年限ギリギリで卒業出来てよかったデス。
・ヨガインストラクター (2021/4/30) (某通信講座の認定証を取得しました。しかし、自分で言うのも何ですが、この資格は全く実を伴っていません。ペーパーだけの資格で非常に取りやすかったです。今後、この資格を復習し、深めていこうと思います)
・国内旅行業務取扱管理者 (2021/10/27)
・TOEIC 600点 (2022/3/20)→ 625点 (2022/8/21) → 700点 (2022/12/18) 2022年のTOEIC三本勝負です。一回目(2022/3/20) 手応えも悪かったが、アクシデントもあったし、今年度中に後2回受けて700点台を狙います。
結果)
手応えはありませんでしたが(出来ないし、最後まで終わらねーなぁ…と)、ギリギリ目標の700点台に乗りました。ゆえに、今回の3本勝負は一応勝利という結果となり良かったデス。
・行政書士 (2023/1/25)
・Riken 物理検定2級 (2024/1/8)
・Riken化学検定準2級(2024/1/22) → 化学検定2級合格へ変更(2024/1/28)
・TOEIC 650点 (2024/5/26) 前回より下がってしまいました…。
・マネジメント検定試験Ⅲ級 (2024/7/15)
・日本語教育能力検定 (2024/12/20)
・秘書技能検定2級 (2025/12/4)
【資格に準ずる扱い】更新 2025.11.18
備忘録的に学校通い等の記録も載せておきます。就職が難しいので学校の方に流れがちです。
*忘れていますが、思い出したら書き加えていきます。
・北海道農業専門学校八紘学園「就農準備校」修了(2005年度)
1ヶ月位だったかな?短期コースに行きました。新潟県の大学を中退後、初めて通った資格ないしスクールがこの就農準備校でした。
・求職者支援訓練「JAVAプロブラミング科」修了(2013年3月28日-2013年9月27日)
プログラミングは難しいといえば難しいですが、自分的にはプログラミングはつまらない感じで適性が無いと思った。この訓練がつまらなく質が低かった、という意味ではない。
・普通職業訓練短期課程「住宅施工技術科」修了(2017年12月1日-2018年5月31日)
住宅施工技術科は失業手当をもらいに行った感じです。
・Le Mark Institute 中退(2025年9月一杯)
インド、ムンバイの写真の学校です。6ヶ月コースに申し込んだのですが1ヵ月で中退しました。本校での影響がブログの今後の写真にも現れてくるかもしれませんね。インド渡航のついでで申し込んだ感じ。「若くないし尚更、写真は自習やオンライン講義でよくない?」と思うでしょうが、↑渡航のついでという事と、学生にモデルをお願いしたかったんですが、頼んでみたら受けてくれたもののそんなに乗り気でもないかな?という感じでした。
【保有日本株式】更新 2025.3.24
現物株(米国株)で再起を図っています。現状日本の株は保有していないです。